Các Cách Chứng Minh Tứ Giác Nội Tiếp THCS Thi Vào 10

Bài toán “Chứng minh tứ giác nội tiếp” chắc chắn đã làm bao thế hệ học sinh phiền não, bởi sự đa dạng trong phương pháp và khó khăn trong nhận định. Tuy nhiên, có một điểm đặc biệt là hiện nay tại các đề toán thi vào lớp 10 hoặc kỳ thi trung học phổ thông đều tồn tại dạng toán này. Hãy cùng kienthuctonghop.vn xin chia sẻ đến bạn đọc các cách chứng minh tư giác nội tiếp chuẩn nhất.

Tìm hiểu những lý thuyết về tứ giác nội tiếp

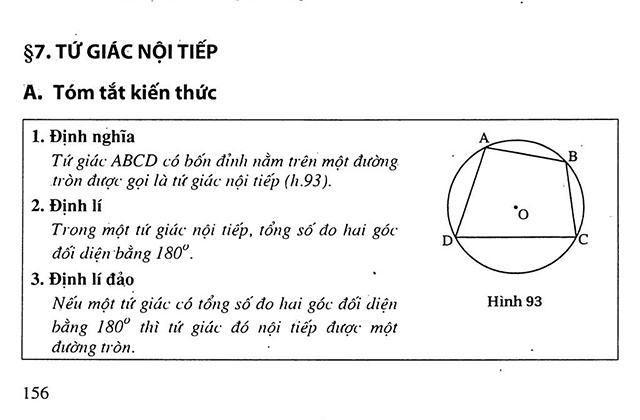
1. Định nghĩa về tứ giác nội tiếp

Tứ giác nội tiếp đường tròn hay tứ giác nội tiếp chính là tứ giác có bốn đỉnh nằm trên cùng một đường tròn. Và đường tròn này được gọi là đường tròn ngoại tiếp tứ giác. 

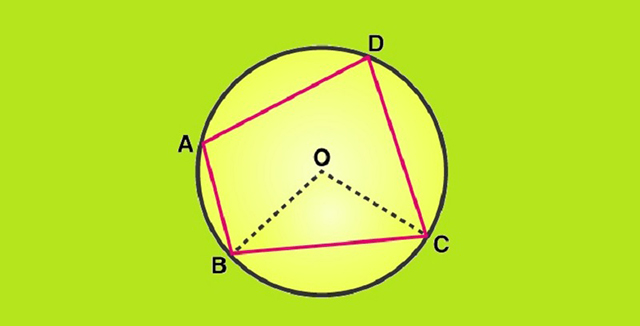
Định nghĩa về tứ giác nội tiếp

2. Các dấu hiệu để nhận biết một tứ giác nội tiếp

Để nhận biết một tứ giác nội tiếp có nội tiếp đường tròn hay không thì chúng ta có thể căn cứ vào các dấu hiệu cơ bản sau đây:

• Tứ giác có tổng số đo của hai góc đối bằng 180 độ thì tứ giác đó nội tiếp một đường tròn.
• Tứ giác có góc ngoài tại một đỉnh bằng với góc trong của đỉnh đối diện thì tứ giác đó sẽ nội tiếp một đường tròn. 
• Tứ giác có bốn đỉnh cách đều một điểm và điểm này sẽ được gọi là tâm đường tròn ngoại tiếp tứ giác. 
• Tứ giác có hai đỉnh kề nhau, cùng nhìn một cạnh chứa hai đỉnh còn lại bằng một góc ∝ thì tứ giác đó sẽ nội tiếp một đường tròn. 

3. Định lý đặc trưng về tứ giác nội tiếp

Một tứ giác nội tiếp đường tròn sẽ có tổng số đo của hai góc đối diện bằng 180 độ. 

4. Định lý đảo để xác định tứ giác nội tiếp

Nếu một tứ giác có tổng số đo của hai góc đối diện bằng 180 độ thì tứ giác đó sẽ nội tiếp một đường tròn.

5. Hệ quả rút ra của tứ giác nội tiếp

Trong một tứ giác nội tiếp, hệ quả gồm:

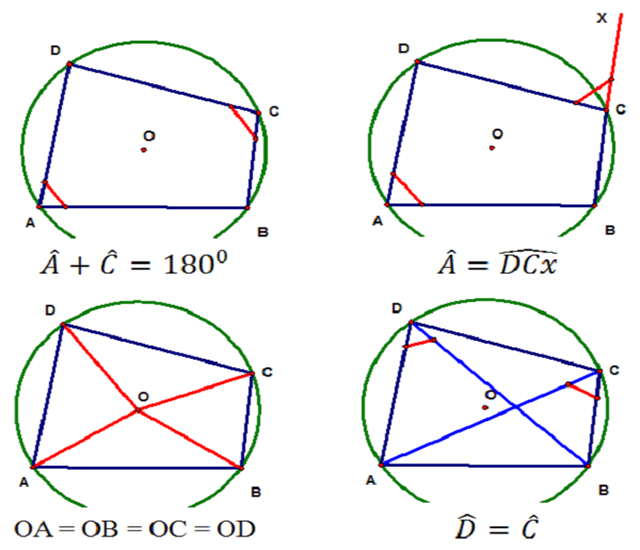
Hệ quả rút ra của tứ giác nội tiếp

• Hai góc nội tiếp khi cùng chắn một cung sẽ bằng nhau.
• Góc nội tiếp sẽ bằng một nửa góc ở tâm khi cùng chắn một cung.
• Góc được tạo bởi đường tiếp tuyến hoặc dây cung sẽ bằng góc nội tiếp cùng chắn một cung. 

Những phương pháp chứng minh tứ giác nội tiếp đường tròn

Căn cứ vào định nghĩa, dấu hiệu cùng các định lý và hệ quả về tứ giác nội tiếp. Dưới đây, chúng tôi xin cung cấp tới bạn đọc 6 phương pháp chứng minh tứ giác nội tiếp đường tròn. Cụ thể như sau:

1. Chứng minh tứ giác có tổng số đo hai góc đối bằng 180 độ

Đây là một phương pháp được căn cứ vào chính định nghĩa về tứ giác nội tiếp. Theo đó, nội dung của cách này sẽ là: “Nếu tứ giác ABCD có tổng số đo của hai góc đối bằng 180 độ thì tứ giác đó sẽ nội tiếp đường tròn”. 

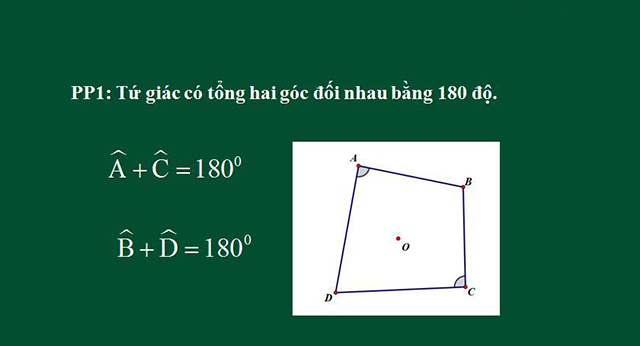
Chứng minh tứ giác có tổng số đo hai góc đối bằng 180 độ

Hệ quả của phương pháp này là : Cho một tứ giác ABCD

• Nếu góc BAD = góc ADC = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O, đường kính BD. 
• Nếu tổng số đo hai góc kề bù EAD = góc BCD thì tứ giác đó cũng nội tiếp đường tròn tâm O. 

2. Chứng minh tứ giác có góc ngoại tại một đỉnh sẽ bằng góc trong tại đỉnh đối diện

Ở phương pháp này, bạn đọc chú ý phải quan sát đúng hình và đúng góc bởi nó rất dễ dẫn đến việc cách chứng minh sai nhưng cho kết quả đúng và ảnh hưởng đến việc làm câu tiếp theo. Cụ thể, cho tứ giác ABCD và khi chứng minh được góc ngoài tại đỉnh A bằng với góc C của tứ giác hoặc góc ngoài tại đỉnh B bằng với góc D của tứ giác thì có thể đưa ra kết luận tứ giác ABCD chính là tứ giác nội tiếp một đường tròn. 

3. Chứng minh hai đỉnh kề nhau và cùng nhìn cạnh đối diện một góc bằng nhau và bằng 90 độ. 

Để áp dụng phương pháp này thì bạn đọc cần chú ý đến dữ kiện mà đề bài đã gợi ý và chứng minh dễ dàng được góc DAC = góc DBC = 90 độ. Từ đó có thể kết luận tứ giác ABCD nội tiếp trong một đường tròn. 

4. Chứng minh bốn đỉnh của tứ giác cùng cách đều một điểm xác định

Khi đề bài cho trước tứ giác ABCD và đường tròn tâm O, bán kính R thì bất cứ một điểm nào nằm trên đường tròn này đều cách tâm O một khoảng đúng bằng bán kính R. Dựa vào tính chất này, bạn có thể dễ dàng chứng minh tứ giác ABCD nội tiếp một đường tròn tâm O và bán kính R.

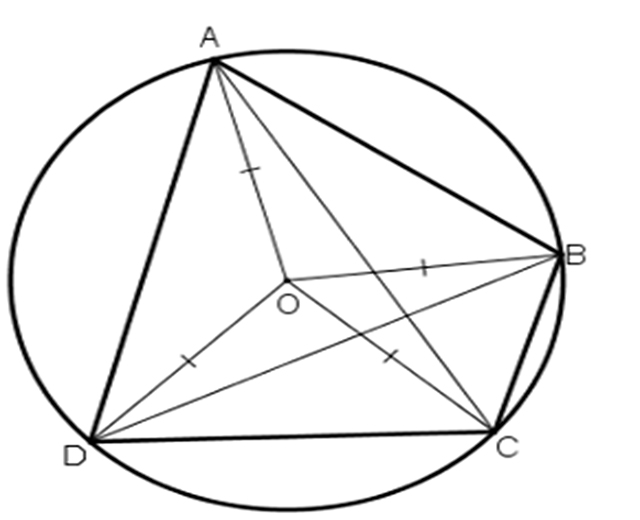
Chứng minh bốn đỉnh của tứ giác cùng cách đều một điểm xác định

Cụ thể, bạn hãy chứng minh bốn điểm A, B, C, D cùng cách đều điểm O và bằng với R; tức là OA = OB = OC = OD = R. Lúc đó, O chính là tâm đường tròn đi qua bốn điểm A, B, C, D hay nói cách khác thì tứ giác ABCD nội tiếp đường tròn tâm O, bán kính R. 

5. Chứng minh tứ giác có tổng số đo hai cặp góc đối diện bằng nhau 

Đây chính là một trường hợp đặc biệt của phương pháp chứng minh thứ hai. Khi đó, nếu cho tứ giác ABCD và nếu chứng minh được tổng số đo hai góc: A + C = B + D thì có thể đưa ra kết luận là tứ giác ABCD nội tiếp trong một đường tròn. 

6. Chứng minh dựa vào phương pháp phản chứng

Đối với phương pháp này, bạn có thể chứng minh tứ giác ABCD được đề bài cho sẵn thành một trong số các hình đặc biệt là hình thang cân, hình chữ nhật và hình vuông. Khi đó, dựa vào tính chất cơ bản của các hình này thì bạn có thể dễ dàng đưa ra kết luận tứ giác ABCD nội tiếp một đường tròn. 

Một số lưu ý cần thiết khi chứng minh tứ giác nội tiếp đường tròn

Khi làm bài chứng minh tứ giác nội tiếp, bạn cần lưu ý các điểm sau đây:

Một số lưu ý cần thiết khi chứng minh tứ giác nội tiếp đường tròn

• Vẽ hình rõ ràng, dễ nhìn, không dính các đường kẻ lên nhau. Ở một số trường hợp đặc biệt không cần thiết vẽ hình để tránh rối hình.
• Các ký hiệu góc hay cạnh bằng nhau cần được xác định và đánh dấu rõ ràng. 
• Bám vào các giả thiết, thông tin đề bài đã cho rồi căn cứ vào kiến thức đã học để tìm phương pháp chứng minh nhanh nhất. 
• Chú ý với các yêu cầu của đề bài sẽ là hướng gợi ý quan trọng để giải quyết bài toán.
• Tuyệt đối không sử dụng các điều đang cần chứng minh để chứng minh lại chúng. 

Bài viết trên đây, chúng tôi đã tổng hợp và chia sẻ thành công đến bạn đọc các cách chứng minh tứ giác nội tiếp. Để trang bị thêm cho mình các kiến thức bổ ích khác, hãy truy cập website kienthuctonghop.vn mỗi ngày nhé!