Tiếp tuyến là gì? Tiếp tuyến là mảng kiến thức quan trọng mà các bạn học sinh được học trong chương trình toán lớp 9. Để biết định nghĩa đường tiếp tuyến là gì? Tính chất và dấu hiệu nhận biết của đường tiếp tuyến như thế nào? Mời các bạn cùng theo dõi bài viết được kienthuctonghop.vn chia sẻ dưới đây!
Nội dung bài viết
Tiếp tuyến là gì?
Theo định nghĩa tiếp tuyến là gì lớp 9 thì đây là đường thẳng chỉ tiếp xúc với đường tròn tại một điểm duy nhất. Đồng thời tiếp tuyến cũng sẽ vuông góc với bán kính đường tròn tại chính điểm đó. Tiếp tuyến của một đường cong là đường thẳng chỉ “chạm” vào đường cong tại một điểm bất kỳ. Tiếp tuyến được vận dụng để xác định độ dốc hay hệ số góc của một đường tại một điểm nhất định dọc theo hướng đó.
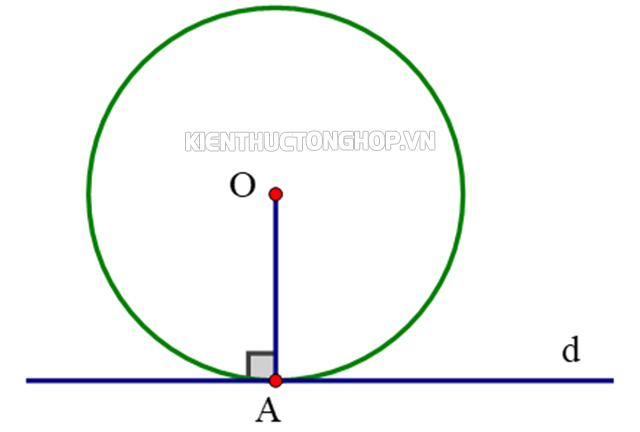
Tiếp tuyến là đường thẳng tiếp xúc với đường tròn tại một điểm duy nhất
Theo Gottfried Leibniz định nghĩa, tiếp tuyến như một đường thẳng nối một cặp điểm gần nhau vô hạn trên đường cong. Chính xác hơn, đường thẳng sẽ là tiếp tuyến của đường cong y = f (x) tại điểm x = c nếu đường thẳng đó đi qua điểm c, f ‘(c) trên đường cong và có độ dốc f ‘(c), f ‘ là đạo hàm của f. Định nghĩa áp dụng cho các đường cong trong không gian Euclide n-chiều.
Dấu hiệu nhận biết tiếp tuyến
Đường thẳng là tiếp tuyến của một đường tròn sẽ có những dấu hiệu nhận biết như sau:
- Nếu một đường thẳng là tiếp tuyến của một đường tròn sẽ vuông góc với bán kính khi đi qua tiếp điểm.
- Nếu một đường thẳng và một đường tròn chỉ có duy nhất một điểm chung thì đường thẳng chính là tiếp tuyến của đường tròn.
- Khoảng cách từ tâm của một đường tròn đến một đường thẳng bất kỳ bằng bán kính của đường tròn thì đường thẳng đó chính là tiếp tuyến.
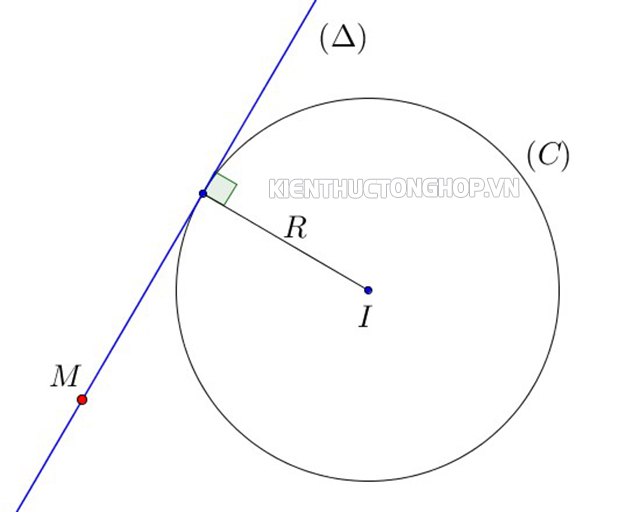
Tiếp tuyến của đường tròn đi qua một điểm duy nhất
Tính chất tiếp tuyến của đường tròn là gì?
Để giải được các bài tập hình học liên quan đến đường tiếp tuyến một cách chính xác, các bạn cần ghi nhớ một số tính chất của tiếp tuyến đường tròn.
- Nếu một đường thẳng được xác định là tiếp tuyến của đường tròn sẽ vuông góc với bán kính đi qua tiếp điểm đó.
- Một đường thẳng khi vuông góc với tiếp tuyến tại điểm tiếp xúc với đường tròn sẽ đi qua tâm.
- Từ một điểm bất kỳ nằm bên ngoài đường tròn, chúng ta luôn vẽ được hai tiếp tuyến với đường tròn đó.
- Hai tiếp tuyến đường tròn sẽ cắt nhau tại 1 điểm bất kỳ và điểm đó chính là khoảng cách cách đều 2 tiếp điểm.
- Nếu hai tiếp tuyến tại A và B trong đường tròn tâm O cắt nhau tại P thì góc BOA và góc BPA bù nhau.
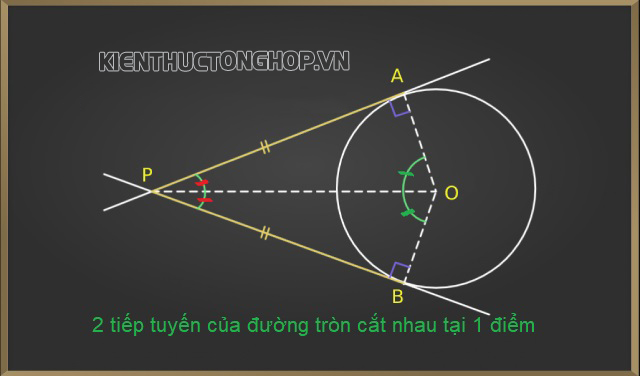
Hai tiếp tuyến đường tròn cắt nhau tại 1 điểm bất kỳ
Phương trình tiếp tuyến đồ thị hàm số
Khi nắm được cách viết phương trình tiếp tuyến là gì, các bạn có thể áp dụng chúng vào việc giải bài tập.
-
Tiếp tuyến vuông góc ⊥ với đường thẳng
Tiếp tuyến d vuông góc với đường thẳng ∆: y = ax + b => ka = -1 => k = -(1/a).
Tóm lại: Phương trình tiếp tuyến d sẽ vuông góc với đường thẳng cho trước với hệ số góc k = -(1/k).
-
Tiếp tuyến // với đường thẳng
Tiếp tuyến d song song với đường thẳng ∆: y = ax + b => k = a.
Phương trình tiếp tuyến d // với đường thẳng cho trước có hệ số góc k = a. Sau khi đã lập được phương trình tiếp tuyến, bạn cần nhớ hãy kiểm tra lại tiếp tuyến đó có trùng với đường thẳng d hay không.
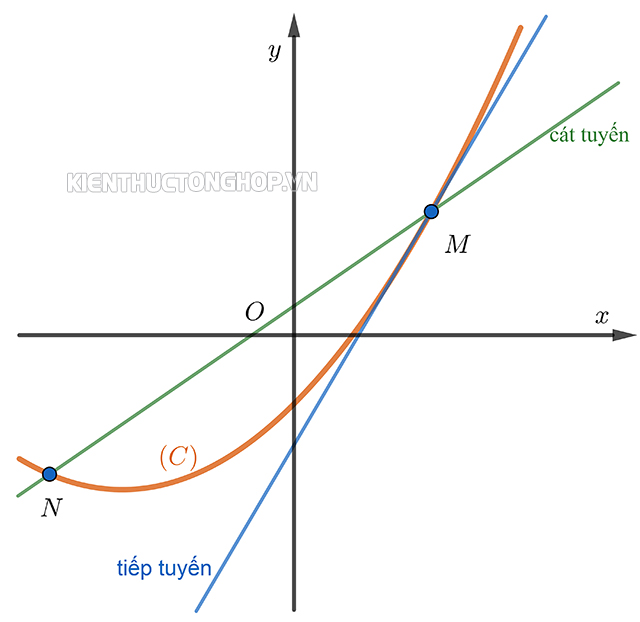
Phương trình tiếp tuyến của đồ thị hàm số tại một điểm
-
Tiếp tuyến tại một điểm
Để viết phương trình tiếp tuyến tại một điểm, ta cần thực hiện theo hai bước:
Bước 1: Tính đạo hàm y’ = f(x) => hệ số góc tiếp tuyến k =y’(x0).
Bước 2: Ta có công thức phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm M(x0,y0 )+y0.
Lưu ý:
- Nếu đề bài cho hoành độ tiếp điểm x0, cần tìm y0 bằng cách thay thế x0 vào hàm số y = f(x0).
- Nếu đề bài cho tung độ tiếp điểm y0, cần tìm y0 thì thay y0 vào hàm số y = f(x0).
- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm đồ thị hàm số (C): y =f(x) với đường thẳng d: y = ax + b. Khi đó, các hoành độ tiếp điểm x chính là nghiệm của phương trình hoành độ giao điểm (C) và d sẽ có dạng: f(x)=ax+b. Nếu trục hoành Ox sẽ có y = 0 và trục tung Oy thì sẽ có x = 0.
Giải thích một số khái niệm liên quan đến tiếp tuyến
Ở phần trên, chúng ta đã cùng nhau tìm hiểu tia tiếp tuyến là gì? Trong phần này, chúng ta tiếp tục khám phá thêm một số khái niệm liên quan đến tiếp tuyến đường tròn nhé!
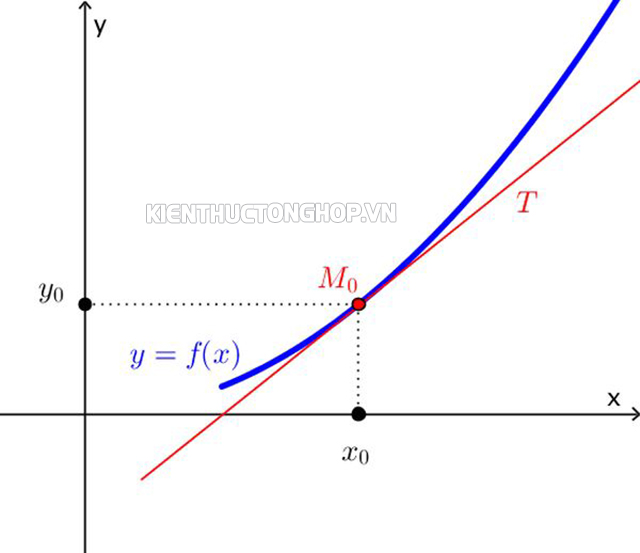
Để tìm tiếp tuyến trong đồ thị hàm số, cần xác định điểm tiếp xúc hay giá trị x0
-
Hệ số góc tiếp tuyến là gì?
Tiếp tuyến đồ thị hàm số tại một điểm chính là đường thẳng tiếp xúc trực tiếp với đồ thị hàm số tại chính điểm đó. Công thức xác định được tiếp tuyến với đồ thị tại một điểm M(x1,x2) là: y=f ′(x1)(x-x1)+ x2. Dựa vào công thức này, chúng ta có thể dễ dàng nhận thấy đạo hàm bậc nhất của hàm số tại hoành độ của điểm, f ′(x0) chính là hệ số góc của đường tiếp tuyến.
-
Gia tốc tiếp tuyến là gì?
Gia tốc tiếp tuyến chính là đại lượng mô tả cho sự thay đổi độ vectơ vận tốc. Gia tốc của tiếp tuyến sẽ có phương trùng với phương của tiếp tuyến. Cùng chiều khi chuyển động nhanh dần hoặc ngược chiều khi chuyển động chậm dần.
Công thức gia tốc tiếp tuyến: at=dvdt.
Chắc hẳn qua bài viết này các bạn đã hiểu rõ hơn về tiếp tuyến là gì cùng một số thông tin liên quan. Hy vọng rằng với những chia sẻ trên đây sẽ giúp ích một phần nào đó giúp các bạn giải bài tập hình học có liên quan.








