Tam giác đồng dạng là khái niệm các bạn học sinh đã được làm quen trong chương trình toán học lớp 8. Bài viết dưới đây sẽ cùng bạn ôn luyện tổng hợp kiến thức hai tam giác đồng dạng về khái niệm cũng như cách chứng minh, phương pháp giải dạng bài này.
Nội dung bài viết
Khái niệm hai tam giác đồng dạng lớp 8
Định nghĩa về tam giác đồng dạng là: Khi một đoạn thẳng cắt hai cạnh của một tam giác bất kỳ và chạy song song với cạnh thứ ba, thì đoạn thẳng đó sẽ tạo thành một tam giác mới đồng dạng với tam giác ban đầu.
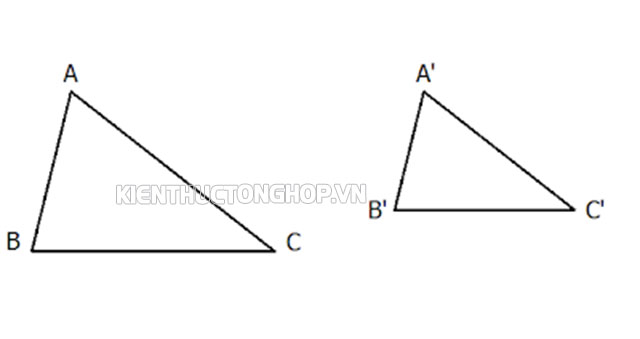
Khái niệm hai tam giác đồng dạng
Cụ thể là tam giác A’B’C’ được xem là đồng dạng tam giác ABC khi thỏa mãn được những điều kiện dưới đây:
- Góc A’ = góc A, góc B’ = góc B, góc C’ = góc C
- Tỉ lệ giữa các cạnh là: A’B/AB = B’C’/BC = A’C’/AC
Kí hiệu tam giác đồng dạng
Ký hiệu tam giác đồng dạng được quy ước là ∼. Nếu tam giác ABC đồng dạng tam giác A’B’C’ ta có ký hiệu như sau: △ABC ∼ △A’B’C’.
Gọi tỉ lệ A’B/AB = A’C’/AC = B’C’/BC = = k. Lúc này, k sẽ được gọi là tỉ số đồng dạng.
Tính chất của tam giác đồng dạng
Xét về tính chất của tam giác đồng dạng, ta có những tính chất như sau:
- Mỗi tam giác đều đồng dạng chính tam giác đó
- Nếu △ABC ∼ △A’B’C’ thì ngược lại, ta cũng có △A’B’C’ ∼ △ABC
- Trong trường hợp hai tam giác đều đồng dạng với một tam giác bất kỳ thì chúng sẽ là các tam giác đồng dạng với nhau. Ví dụ: △ABC ∼ △A’B’C’, mặt khác ta cũng có △A”B”C” ∼ △A’B’C’ suy ra △ABC ∼ △A”B”C”.
- Tỉ số diện tích của 2 tam giác đồng dạng sẽ bằng bình phương của tỉ số đồng dạng.
Mặt khác, nếu hai tam giác bằng nhau cũng sẽ đồng dạng với nhau. Nhưng hai tam giác đồng dạng nhau thì không phải lúc nào nó cũng sẽ bằng nhau
Các trường hợp tam giác đồng dạng
Sau đây là những trường hợp đồng dạng tam giác mà các bạn học sinh cần phải nắm vững để vận dụng linh hoạt trong các bài tập.
Trường hợp 2 cạnh tỉ lệ cạnh – cạnh – cạnh
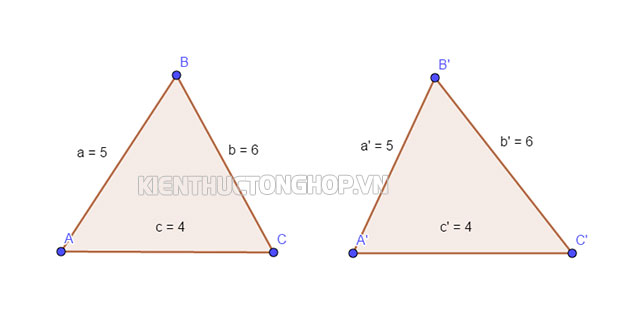
Tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh
Đối với trường hợp tỷ lệ cạnh – cạnh – cạnh (viết tắt là c.c.c) thì ta có thể phát biểu thành lời như sau:
Nếu ba cạnh một tam giác bất kỳ tỉ lệ tương ứng với ba cạnh của một tam giác khác thì hai tam giác đó được gọi là đồng dạng với nhau, theo quy tắc cạnh – cạnh – cạnh.
Trường hợp góc và 2 cạnh liền kề nhau cạnh – góc – cạnh (c.g.c)
Trong trường hợp góc – cạnh – góc (nghĩa là xét một góc và hai cạnh kề của góc đó), ta có khẳng định dưới đây:
Nếu hai cạnh của một tam giác này tỷ lệ tương ứng với hai cạnh của một tam giác khác, và hai góc được hình thành bởi hai cặp cạnh này có giá trị bằng nhau, thì hai tam giác đó được coi là đồng dạng với nhau theo nguyên tắc cạnh – góc – cạnh
Trường hợp 3 góc bằng nhau Góc – Góc
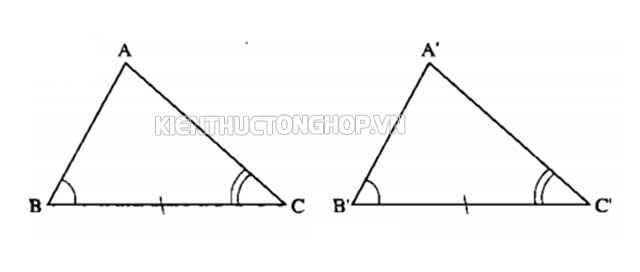
Tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh
Một trường hợp đồng dạng khác trong tam giác mà bạn cũng cần ghi nhớ là trường hợp góc – góc (viết tắt là g.g). Trong trường hợp này, ta có câu phát biểu sau:
Nếu hai góc của một tam giác bất kỳ có số đo bằng với hai góc của một tam giác khác, thì ta nói rằng hai tam giác này đồng dạng với nhau theo quy tắc góc – góc.
Tổng hợp các phương pháp chứng minh hai tam giác đồng dạng toán lớp 8
Để chứng minh hai tam giác đồng dạng, ta có thể áp dụng các phương pháp sau:

Cách chứng minh hai tam giác đồng dạng
Phương pháp 1: Hai tam giác được xem là đồng dạng nếu chúng có cặp cạnh tương ứng tỉ lệ và các góc tương ứng bằng nhau.
Phương pháp 2: Định lý Talet: Nếu một đường thẳng song song một cạnh của tam giác và cắt hai cạnh còn lại sẽ vạch ra trên cạnh đó những đoạn thẳng tương ứng tỷ lệ.
Phương pháp 3: Chứng minh các điều kiện cần và đủ để hai tam giác đồng dạng:
- Cặp cạnh tương ứng tỷ lệ thì đồng dạng.
- Hai cặp góc tương ứng bằng nhau thì đồng dạng.
- Hai cặp cạnh tương ứng tỷ lệ, và góc xen giữa hai cặp cạnh đó bằng nhau thì đồng dạng.
Ứng dụng thực tế của tam giác đồng dạng
Nguyên tắc đồng dạng tam giác có ứng dụng rộng rãi trong nhiều lĩnh vực thực tế, bao gồm hình học, kỹ thuật, địa chất, thiết kế, và nhiều lĩnh vực khác. Dưới đây là một số ứng dụng cụ thể của nguyên tắc đồng dạng tam giác trong cuộc sống hàng ngày:
- Bản đồ và hệ thống định vị: Trong địa lý, nguyên tắc đồng dạng tam giác được áp dụng để xây dựng bản đồ và hệ thống định vị, như hệ thống GPS, để xác định vị trí và khoảng cách giữa các điểm trên bản đồ.
- Kiến trúc và thiết kế: Trong kiến trúc và thiết kế, nguyên tắc đồng dạng tam giác giúp các kiến trúc sư và nhà thiết kế tạo ra các mô hình và bản vẽ thể hiện kích thước và tỷ lệ của các chi tiết.
- Trắc địa và xây dựng: Trong trắc địa và xây dựng, nguyên tắc đồng dạng tam giác được sử dụng để đo và tính toán khoảng cách, kích thước và độ nghiêng của các cấu trúc xây dựng.
- Định hướng và định vị trong không gian: Trong hàng không và hải quân, nguyên tắc đồng dạng tam giác giúp xác định hướng, vị trí và khoảng cách của các đối tượng trong không gian.
- Hình dáng và đo lường: Các nguyên tắc đồng dạng tam giác cũng được sử dụng trong việc đo lường và tính toán kích thước của các đối tượng, chẳng hạn như đo chiều cao của một tòa nhà hoặc khoảng cách giữa hai điểm trên một bản đồ.
- Thiết kế đồ họa và 3D: Trong thiết kế đồ họa và 3D, nguyên tắc đồng dạng tam giác được sử dụng để tái tạo các hình dạng và đối tượng trong môi trường số hóa.
Dạng bài tập về hai tam giác đồng dạng
Dưới đây là một số dạng bài tập thường gặp liên quan đến tam giác đồng dạng. Bạn có thể tham khảo để ôn tập và làm tốt các bài tập có liên quan.

Dạng bài tập liên quan về tam giác đồng dạng
Bài 1: Cho △DEF và △D’E’F’. △DEF ∼ △D’E’F’ khi:
- A. Góc D = góc D’, góc E = góc E’
- B. Góc D = góc E, góc D’ = góc E’
- C. Góc D = góc F, góc D’ = góc CF’
- D. Tất cả các trường hợp trên đều sai
Đáp án: A. Góc D = góc D’, góc E = góc E’
Bài 2: Phát biểu nào sau đây là sai?
- A. Mỗi tam giác đều đồng dạng với chính nó.
- B. Nếu △DEF ∼ △D’E’F’ thì ngược lại ta có, △D’E’F’ ∼ △DEF.
- C. Trong một tam giác, đường phân giác của một góc bất kỳ sẽ chia cạnh đối diện thành hai đoạn thẳng không tỉ lệ với hai cạnh kề của hai đoạn ấy.
- D. k không được gọi là tỉ số đồng dạng khi k = D’E/DE = E’F’/EF = D’F’/DF.
Đáp án: C. Trong một tam giác, đường phân giác của một góc bất kỳ sẽ chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn ấy.
Qua bài viết này, chúng ta đã cùng ôn tập và tổng hợp kiến thức về tam giác đồng dạng, từ khái niệm cơ bản đến phương pháp chứng minh và giải các dạng bài liên quan. Chúc các bạn học sinh ôn tập tốt và tự tin giải bài tập về dạng này.
>>> Xem thêm cách quy đổi 1 feet bằng bao nhiêu cm chỉ 1 bước cực nhanh










