Hình chóp, hình chóp đều là kiến thức hình học quan trọng mà các bạn học sinh cần được nắm vững trong chương trình toán học lớp 8. Những thông tin qua bài viết sau sẽ tổng hợp kiến thức về hình chóp – Khái niệm, tính chất và cách làm dạng bài này.
Nội dung bài viết
- Hình chóp là gì? Hình chóp đều là gì?
- Các loại hình chóp đều thường gặp
- Hình chóp có những tính chất gì?
- Công thức tính chu vi hình chóp
- Công thức tính diện tích xung quanh hình chóp
- Công thức tính diện tích toàn phần của hình chóp
- Công thức tính thể tích hình chóp
- Công thức tính diện tích mặt cầu ngoại tiếp hình chóp
- Một vài lưu ý khi tính chu vi, diện tích và thể tích hình chóp
Hình chóp là gì? Hình chóp đều là gì?
Trong hình học, hình chóp được định nghĩa là một khối đa diện được tạo thành bằng cách kết nối một điểm của một đa giác và một điểm, được gọi là đỉnh. Mỗi cạnh của đáy và đỉnh chóp tạo thành một hình tam giác, được gọi là mặt bên. Một hình chóp có đáy là đa giác n cạnh sẽ có n + 1 đỉnh, n + 1 mặt và 2n cạnh.
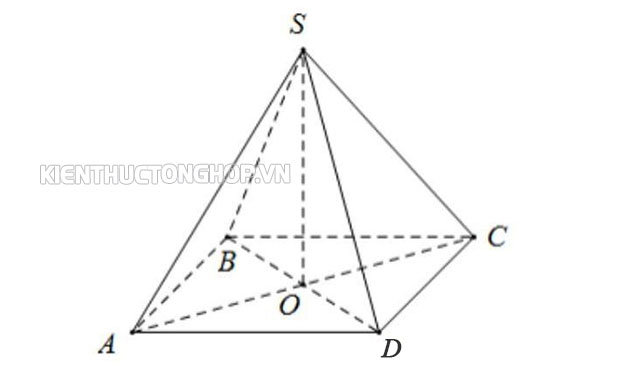
Cho hình chóp S.ABCD
Hình chóp có nhiều hình dạng khác nhau, và tên của nó thường được xác định dựa trên hình dạng của đáy. Ví dụ, hình chóp có đáy là một hình tam giác được gọi là “hình chóp tam giác”, và khi đáy là một hình tứ giác, ta gọi là “hình chóp tứ giác”.
Trong trường hợp đặc biệt khi đáy là một tam giác đều hoặc tứ giác đều, ta gọi hình chóp đó là “hình chóp đều”.
Hiểu một cách đơn giản, hình chóp là một dạng khối đa diện có đáy là một đa giác lồi và các mặt bên của tam giác cùng chung một đỉnh.
Các loại hình chóp đều thường gặp
Dựa trên hình dạng của đáy, hình chóp đều được phân thành các loại khác nhau như sau:
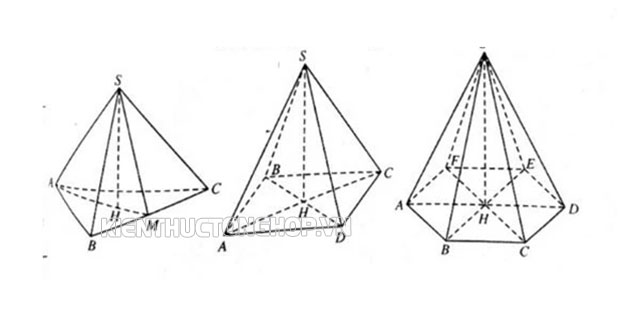
Các loại hình chóp đều thường gặp
Hình chóp đa giác đều
Đây là hình chóp mà đáy của nó là một đa giác đều. Các mặt bên của hình chóp này đều bằng nhau. Đáy của hình chóp đa giác đều có thể là hình vuông, hình tam giác đều, hình lục giác đều… Trọng tâm của đáy trùng với chân đường cao của hình chóp.
Hình chóp tứ giác đều
Hình chóp có đáy là hình vuông, các mặt bên là những tam giác cân bằng nhau, chung đỉnh nên được gọi là hình chóp tứ giác đều. Hình chóp tứ giác đều có 8 cạnh, và các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau.
Hình chóp tam giác đều
Đây là hình chóp có đáy là tam giác đều, các mặt bên đều là tam giác cân bằng nhau có chung đỉnh. Tâm đáy là trọng tâm tam giác và cũng là chân đường cao. Các mặt bên hình chóp đều là các tam giác cân bằng nhau và các cạnh của chúng bằng nhau.
Hình chóp có những tính chất gì?
Dưới đây là những tính chất cơ bản của hình học này:
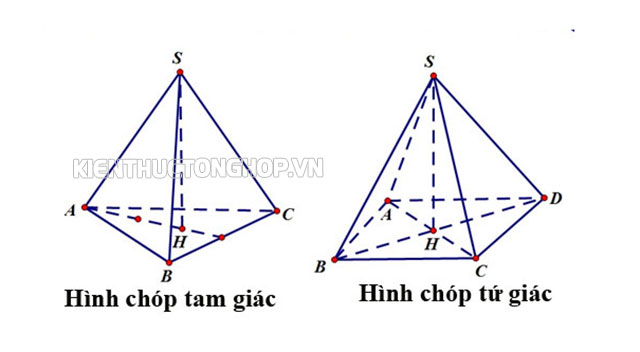
Tên của hình chóp dựa vào loại đa giác đáy
- Đường thẳng đi qua đỉnh của hình chóp và hợp với mặt phẳng đáy được gọi là đường cao của hình chóp.
- Tên của hình chóp thường dựa vào loại đa giác của đáy. Ví dụ, khi đáy là một tam giác, ta gọi hình đó là “hình chóp tam giác”. Khi đáy là một tứ giác, ta gọi hình đó là “hình chóp tứ giác”.
- Nếu các cạnh và góc của hình chóp đều bằng nhau, hoặc nếu các cạnh bên của hình chóp bằng nhau, thì chân đường cao có thể là tâm của đường tròn ngoại tiếp đáy.
- Trong trường hợp tâm hình chóp có các cạnh tạo với đáy những góc bằng nhau hoặc chiều cao của các cạnh xuất phát từ một đỉnh bằng nhau, thì gốc của đường cao sẽ trùng với tâm của đường tròn nội tiếp đáy.
- Nếu hình chóp có mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy, thì đường cao của hình chóp sẽ trùng với đường cao của mặt bên hoặc mặt chéo đó.
Công thức tính chu vi hình chóp
Chu vi của hình chóp được tính bằng tổng chu vi của các mặt bên và mặt đáy. Công thức tính chu vi được biểu diễn như sau:
P = P các mặt bên + P mặt đáy. Trong đó:
- P: chu vi hình chóp
- P mặt bên: Tổng chu vi của các mặt bên của hình chóp
Ví dụ: Ví dụ, nếu bạn có một hình chóp có đáy là hình vuông với cạnh a và các mặt bên là các tam giác cân, thì chu vi của hình chóp có thể được tính bằng:
P = 4x Pmặt bên + P đáy. Trong trường hợp này, bạn cần tính chu vi của các tam giác bên và chu vi của hình vuông đáy để tính toán tổng chu vi của hình chóp.
Công thức tính diện tích xung quanh hình chóp
Diện tích xung quanh của một hình chóp đều được tính bằng tích nửa chu vi mặt đáy nhân với trung đoạn.
Công thức Sxq = P/2 x d
Trong đó:
- Sxp: Diện tích xung quanh của hình chóp
- P/2: Nửa chu vi của đáy
- d: Độ dài của trung đoạn từ đỉnh của mặt bên đến tâm của đáy.
Công thức tính diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp thường được tính bằng cách tổng hợp diện tích của mặt đáy và diện tích xung quanh (bề mặt bên).
Công thức: Stp = Sxq + Sđáy
Trong đó:
- Sxq: Diện tích xung quanh của hình chóp
- Sđáy: Diện tích đáy của hình chóp.
Công thức tính thể tích hình chóp
Thể tích của hình chóp được tính bằng bằng 1/3 diện tích mặt đáy nhân với chiều cao.
Công thức tính như sau: V = 1/3 S.đáy x h
Trong đó:
- V: Thể tích của hình chóp
- S.đáy: Diện tích đáy hình chóp
- h: Chiều cao.
Công thức tính diện tích mặt cầu ngoại tiếp hình chóp
Mặt cầu là tập hợp điểm M có trong không gian cách điểm O cố định một khoảng R gọi là tâm cầu O, bán kính R, kí hiệu: S(O; R) hay {M/OM = R}, vậy công thức tính diện tích mặt cầu ngoại tiếp như sau:
Công thức: S = 4 x π x R^2.
Trong đó
- S: Kí hiệu diện tích mặt cầu
- R: bán kính mặt cầu ngoại tiếp
Một vài lưu ý khi tính chu vi, diện tích và thể tích hình chóp
Khi làm các dạng bài tập về hình chóp, có một số lưu ý quan trọng bạn nên cân nhắc:

Lưu ý khi làm dạng bài về hình chóp
- Hiểu rõ đề bài: Đầu tiên, đảm bảo bạn đã hiểu rõ yêu cầu của đề bài. Xác định hình dạng của hình chóp, các thông số đã cho và những gì bạn cần tính toán.
- Phân loại hình chóp: Xác định loại hình chóp liên quan đến đáy (hình vuông, tam giác, đa giác đều) và cách các mặt bên nối với đỉnh chóp.
- Sử dụng công thức chính xác: Dựa vào loại hình chóp và thông số đã cho, áp dụng các công thức tương ứng cho chu vi, diện tích, và thể tích. Chắc chắn rằng bạn sử dụng đúng công thức và thay đủ thông số vào chúng.
- Chuyển đổi đơn vị: Kiểm tra xem các đơn vị đo có nhất quán hay không. Nếu cần, chuyển đổi chúng thành cùng một đơn vị để tính toán dễ dàng và chính xác hơn.
Để làm thành thạo, hãy làm nhiều bài tập khác nhau liên quan đến hình chóp. Điều này sẽ giúp bạn nắm vững kiến thức và phát triển tư duy giải quyết các dạng bài tập liên quan.
Trên đây là tổng hợp kiến thức, công thức liên quan về hình chóp. Mong rằng sẽ giúp ích cho việc tổng hợp, ôn luyện của bạn dễ dàng hơn. Nếu còn vấn đề gì chưa hiểu về hình học này, bạn đọc có thể để lại bình luận dưới bài viết để mọi người cùng giúp đỡ nhé!










